Intro
Very often we need to generate random numbers for different purposes ranging from simple games to advances encryption algorithms.
Many C/C++ programmers are well used with the srand() / rand() functions, but simply using a predefined code to achieve the given tasks, is sometimes not enough.
Fully understanding what a random number is, how it can be generated, helps getting the best solution.
Starting with my first university years, I used a linear pseudorandom generator, easy to implement, and quite useful in many applications.
A pseudorandom number generator (PRNG) is an algorithm for generating a sequence of numbers that approximates the properties of random numbers. The sequence is not truly random in that it is completely determined by a relatively small set of initial values, called the PRNG’s state. Read more here.
A simple approach
Let’s consider a,b and c three integer constant. We plan to generate a set of pseudorandom numbers X0, X1, … , Xn. Assuming X0 = d, the rest of the numbers can be computed in a recurrent using the formula:
Xn+1 = (a*Xn + b) % c .
a,b,c and d are the initial values, also known as the PRNG’s state.
c limits the resulting values to the interval 0.. c-1
a and b are affecting the linear angle.
Here is a simple C algorithm to better illustrate the formula:
#include
int main()
{
int a=71, b=19, c=256, d = 3;int x[200] , i = 0;
x[0] = d;
for (i=1;i<200;i++) x[i] = (a*x[i-1] + b) % c; printf("The pseudo random numbers are:\n"); for (i=0;i<200;i++) printf("%d ", x[i]); return 1; }
You can see the result in the following image:
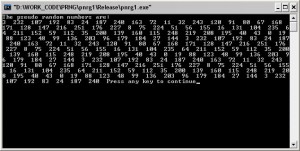
Source code here:pnrg1.
To resemble the srand() and rand() functions you’re all used to, I need to highlight that they’re also using a PRNG. srand() “seeds” the random generator and practically all that does is to set the initial values (PRNG’s state).
You can easily adapt the generator above to work like srand() and rand():
#include
int a = 71,b = 19, d = 0;
void mysrand(int seed)
{
d = seed;
}int myrand(int threshold)
{
int x = d;
x = (a*x + b) % threshold;
d = x; // advance with each function call
return x;
}void main()
{
mysrand(122);
printf(“PseudoRandom number: %d\n”, myrand(256));
printf(“PseudoRandom number: %d\n”, myrand(256));}
Result as pictured below:
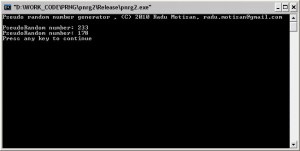
The source code here: pnrg2
You’ll quickly notice that the PRNG produces the same output every time you initialize the mysrand with the same value:
mysrand(122) -> myrand(256)=233
But this is the same in the case of the built in srand() and rand() function too. The reason is that we don’t have a good source for chaos. You can overcome this by using:
mysrand(GetTickCount());
or
mysrand(Cursorpos.x)
or
mysrand(FreeRAMMemory())
or
mysrand(UserLastKeyPressed)
or etc, linking the initialization function to a random event.
Further analysis
Talking about the chaos level of this generator, there is a simple way of analyzing a sequence of numbers, in our case the X0,…,Xn serie outputed by the linear PRNG.
1. In a single dimensioned space, represented by the real number axis and the corresponding set of all real numbers (R), a given number can be viewed as a single entity corresponding to a point on the axis.
For eg., see the following picture:
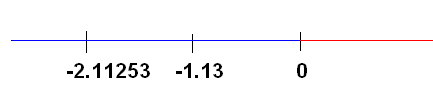
It represents a few real numbers on the axis. One might ask, what’s the meaning of number -1.13 . The simple answer is: -1.13 is the entity that sits on the axis at the given position. Several properties can be extrapolated, and we get a meaning of what -1.13 is, and most important: what can we do with it.
2. For a given pair of numbers, we can image a bidimensional space, where the pair represents a point in a Cartesian system of reference. The pair receives a meaning, and we can further elaborate on that, using the pair for various purposes.
In a similar way, for a given set of numbers (x0,x1,…,xn) that seem random and meaningless at first, let’s not forget that in a n-dimensional space, the set of numbers has a very simple and clear meaning: it represents a point.
Luckily, for the PRNG’s the things are simpler.
Given a set of numbers generated with the linear PRNG, they can be represented without any meaning in one dimension: they would be “random” points on the number axis.
BUT, we can search for a “path” or a “meaning” by moving to a superior space, in this case to two dimensions, and representing the pseudo numbers set by point of coordinates (Xn-1, Xn).
See the following sample:
1- The first PRNG sample I’ve posted, produced the following numbers:
3 232 107 192 83 24 187 240 163 72 11 32 243 120 91 80 67 168 …. etc
It is very hard to understand what these numbers mean or to give a purpose to this sequence or even to understand the pattern that served to produce them.
2- Let’s write a simple program to graphically illustrate in two dimensions pairs of numbers (Xn, Xn+1) as points in a Cartesian system.
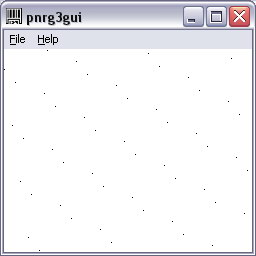
The points in the picture are nothing else then the 200 pseudo random numbers (3 232 107 192 83 24 187 240 163 72 11 32 243 120 91 80 67 168
171 128 147 216 251 176 227 8 75 224 51 56 155 16 131 104 235 6
4 211 152 59 112 35 200 139 160 115 248 219 208 195 40 43 0 19
88 123 48 99 136 203 96 179 184 27 144 3 232 107 192 83 24 187
240 163 72 11 32 243 120 91 80 67 168 171 128 147 216 251 176
227 8 75 224 51 56 155 16 131 104 235 64 211 152 59 112 35 200
139 160 115 248 219 208 195 40 43 0 19 88 123 48 99 136 203 9
6 179 184 27 144 3 232 107 192 83 24 187 240 163 72 11 32 243
120 91 80 67 168 171 128 147 216 251 176 227 8 75 224 51 56 155
16 131 104 235 64 211 152 59 112 35 200 139 160 115 248 219 20
8 195 40 43 0 19 88 123 48 99 136 203 96 179 184 27 144 3 232
107 192 83 24 187 240)
Interestingly, what at first seemed total chaos, now reminds the proper order of a orchard with trees properly planted in rows and columns, at a given angle, in our image represented by the black dots.
Get the source code here: pnrg3gui
If viewing the sequence in two dimensions doesn’t show anything useful, we can move further and check the representation in three dimensions, points of coordinates (Xn-1, Xn, Xn+1), and so on.
As shown above, at one given level, the “random” content will get a meaning.
Hope this helps,
Radu
